算法导论读书笔记(5)

计数排序（Counting Sort）

<p align="center">

</p>

资料来源:维基百科    Lazy pig    «算法导论»

译:计算机科学中，计数排序是一类更具有小值的数字来存储排序的一类算法。是整数排序算法。具体是根据现有的关键值，根据累计的方法来确定每一个值出现的次数，从而根据其次数进行放置位置。它的运行时间是线性的（在最大数和最小数之间）。所以运用范围是当值都比较小的时候。但是，这可以运用到另一个排序算法中——基数排序，它能更有效地排更大的数字。

计数排序不是比较排序，它的下界是nlgn，桶排序则是运用多次的这样的方式实现的。但是，相对于计数排序来说，桶排序需要链表，动态数组，这需要耗费内存来存储。

图示:

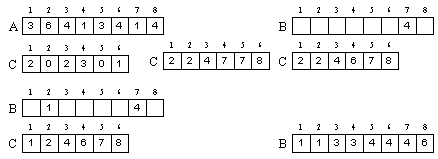
伪代码：

COUNTING-SORT(A, B, k)
1  let C[0 .. k] be a new array
2  for i = 0 to k
3      C[i] = 0
4  for j = 1 to A.length
5      C[A[j]] = C[A[j]] + 1
6  // C[i] now contains the number of elements equal to i.
7  for i = 1 to k
8      C[i] = C[i] + C[i - 1]
9  // C[i] now contains the number of elements less than or equal to i.
10 for j = A.length downto 1
11     B[C[A[j]]] = A[j]
12     C[A[j]] = C[A[j]] - 1

解释：本算法需要3个数组

A：用来存放最初始的数组

C：用来进行计数并累加 中间变换较多

B： 用来存放以排序的数组

1-2行：创建新数组，把C数组都清零。

4-5行：把A[i]作为C的下标，证明是在计算在A[i]下标位置下出现的次数。

7-8行：将C中的数字向后进行累加

10-12行：下标是从高位走向地位，

B[C[A[j]]] = A[j]

这一段代表把A第j+1一个元素放在，下标是A[j]的C数组的元素，再将得到的那个累加得到的元素作为下标放在B元素里面。

C[A[j]] = C[A[j]] - 1

C中下标是A[J]的那个元素次数-1

代码实现：

#include <iostream>

int * countingSort(int * array) {
	int * result = new int[10];
	int * temp = new int[10];
	for (int i = 0; i < 10; i++)
		temp[i] = 0;
	for (int j = 0; j < 10; j++)
		temp[array[j]]++;
	for (int i = 1; i < 10; i++)
		temp[i] = temp[i] + temp[i - 1];
	for (int j = 10 - 1; j >= 0; j--) {
		result[temp[array[j]] - 1] = array[j];
		temp[array[j]]--;
	}
	return result;
}
void main(){
	using namespace std;
	int A[10] = { 0, 9, 8, 7, 6, 5, 4, 3, 2, 1 };
	int *B;
	B = countingSort(A);
	for (int i = 0; i < 10; i++){
		cout << B[i] << " ";
	}
	system("pause");
}

桶排序

当 桶排序 （bucket sort）的输入符合均匀分布时，它可以以线性时间运行。桶排序假设输入由一个随机过程产生，该过程将元素均匀地分布在区间[ 0， 1 )上。

桶排序的思想就是把区间[ 0， 1 )划分成 n 个相同大小的子区间，或称 桶 。然后，将 n 个输入数分布到各个桶中去。因为输入数均匀分布在[ 0， 1 )上，所以，一般不会有很多数落在一个桶中的情况。为得到结果，先对各个桶中的元素进行排序，然后按次序把桶中的元素列出来即可。

BUCKET-SORT(A) 1 let B[0 .. n - 1] be a new array 2 n = A.length 3 for i = 0 to n - 1 4 make B[i] an empty list 5 for i = 1 to n 6 insert A[i] into list B[FLOOR(nA[i])] 7 for i = 0 to n - 1 8 sort list B[i] with insertion sort 9 concatenate the lists B[0], B[1], ..., B[n - 1] together in order